Re: gEDA-user: terminators

[Steven Michalske <smichalske@xxxxxxxxx>]

   On Apr 7, 2009, at 10:48 AM, [1]carzrgr8@xxxxxxxxxxxxx wrote:

   ----- Original Message -----
   From: John Griessen

     [jg]I think HJ might have meant length of the ramp up or ramp

     down when he said "edge".

     I can't see how length of a square wave half cycle translates

     to fractions of wavelengths  at some resonance...which is where
     "1/4 * 'length of the

   edge'"   must come from.

   i was using a sine wave to approximate the triangle wave from perfect
   ramps up and perfect ramps down, (full cycles, not half. ), cutting
   out the rest periods to simplify the math.

   Yep, it's the edge not the cycle.  A 1ns edge has 500 MHz component.
   That's true even
   if the square wave were 1 kHz.

    If you think you don't have a transmission line for that
   example, you'd be wrong.  That 1nS edge will rattle around on a long
   trace if not
   terminated.  You'd see it as ringing.  By saying 1/4 length of the
   edge is the longest you
   can go without termination means that all the ratling due to
   reflections is damped out long
   before the edge reaches it's full value.

   This math is why a 3 inch trace woulden't
   The 500 MHz component for a 1kHZ clock is at 1/500000th the energy.
    or 3.3 volts * 2E-6 or 6.6 micro volts.
   IF and only IF it has a 0 second edge rate.

   Guy's,
   I'm trying to keep it to rules of thumb, that my co workers and I use
   to build computers with the latest ram and IO technologies.
   USB2,  at 480 mbps,  aww, short stubs,  match the impedance keep them
   close and not care.  From doctorates in the field and have years
   of experience.
   no parts you are using are really square waves, they are trapezoidal.
   you can't just look at the ramp from the edge, your sending a series,
   and they sum up constructively or destructively, on the bounce back.
   the mismatched impedance interfaces are also not perfect reflectors.
   ( I'm not pulling the reflection coefficient in to this. )
   now to defend my rule of thumb,
   it's not just the edge, it is the whole standing wave.  take the
   Fourier series below,  from mathworld
   [2]http://mathworld.wolfram.com/FourierSeries.html
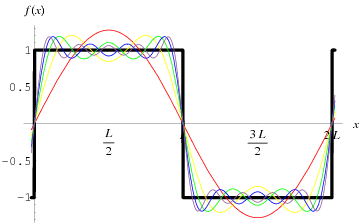
   FourierSeriesSquareWave
   take your Fourier series and expand it till you get a sum of sine
   waves matching your edge.  thats all the content you need,  the higher
   order harmonics aren't a significant part of your energy, they are
   there but they drop off rapidly.   a 1/n relationship from the series.
    and square waves only include odd harmonics of the waveform.
   133MHz   at full strength
   399MHz  at 1/3rd the energy
   665MHz at 1/5th the energy
   931MHz at 1/7th the energy
   1.197 GHz at 1/9th the energy   <-  nearly nonexistent on DJ's
   transmission lines, any radio card guys want to explain why?
   these lines are lossy so the energy gets absorbed in the lines, the
   SWR  is low because the lines are short.
   now if you treat it as a ramp,  you have a whole different set
   of Fourier sums that are required to make it start at the bottom and
   stay at the top.  I'm not getting in to that math because it's
   not relevant in a clocked periodic system.
   DJ is building a 133MHz, and its a medium speed interface,  slow edges
   will help him,  making his timing meet the specifications of his
   memory will help him
   use the speed of light in a vacuum  and 1/8th wave antenna.
   use the speed of light on FR4 and a 1/4 wave antenna.
   they equate.

References

   1. mailto:carzrgr8@xxxxxxxxxxxxx
   2. http://mathworld.wolfram.com/FourierSeries.html

_______________________________________________
geda-user mailing list
geda-user@xxxxxxxxxxxxxx
http://www.seul.org/cgi-bin/mailman/listinfo/geda-user